Ontdek de Wondere Wereld van de Driehoek
Wat is een driehoek? Deze ogenschijnlijk eenvoudige vraag opent de deur naar een wereld van geometrische wonderen. Van de piramides van Egypte tot de moderne architectuur, de driehoek speelt een cruciale rol in ons begrip van de wereld om ons heen. Laten we samen op ontdekkingstocht gaan en de geheimen van deze fundamentele vorm ontrafelen.
Een driehoek is meer dan alleen een simpele tekening. Het is een bouwsteen van complexe structuren, een symbool van kracht en stabiliteit, en een bron van eindeloze wiskundige exploratie. De driehoek is een veelhoek met drie zijden en drie hoeken. Deze eenvoudige definitie vormt de basis voor een breed scala aan toepassingen in wetenschap, technologie, engineering en kunst.
De driehoek, een vorm die al eeuwenlang de mens fascineert, is een fundamenteel concept in de geometrie. Vanaf de vroegste beschavingen, die de driehoek gebruikten voor landmeting en bouw, tot de moderne wiskunde, waar het een sleutelrol speelt in complexe berekeningen, is de driehoek altijd een bron van studie en inspiratie geweest. Wat maakt deze vorm zo bijzonder? Laten we dieper duiken in de wereld van de driehoek.
De vraag "Wat is de driehoek?" kan op verschillende manieren worden beantwoord. We kunnen kijken naar de wiskundige definitie: een gesloten figuur met drie zijden en drie hoeken. We kunnen kijken naar de praktische toepassingen: van de constructie van bruggen tot het ontwerp van kunstwerken. En we kunnen kijken naar de symbolische betekenis: de driehoek als representatie van stabiliteit, kracht en harmonie.
De essentie van de driehoek ligt in zijn eenvoud en tegelijkertijd zijn complexiteit. Het is een vorm die gemakkelijk te tekenen en te begrijpen is, maar die tegelijkertijd de basis vormt voor complexe geometrische berekeningen en constructies. In de volgende paragrafen zullen we de verschillende aspecten van de driehoek verder verkennen.
De geschiedenis van de driehoek gaat terug tot de oudheid. Babylonische en Egyptische beschavingen gebruikten al kennis van driehoeken voor landmeting en bouwwerken. De Griekse wiskundige Euclides legde de basis voor de formele studie van de driehoek in zijn werk "Elementen".
Een belangrijk aspect van de driehoek is de stelling van Pythagoras, die de relatie beschrijft tussen de lengtes van de zijden in een rechthoekige driehoek.
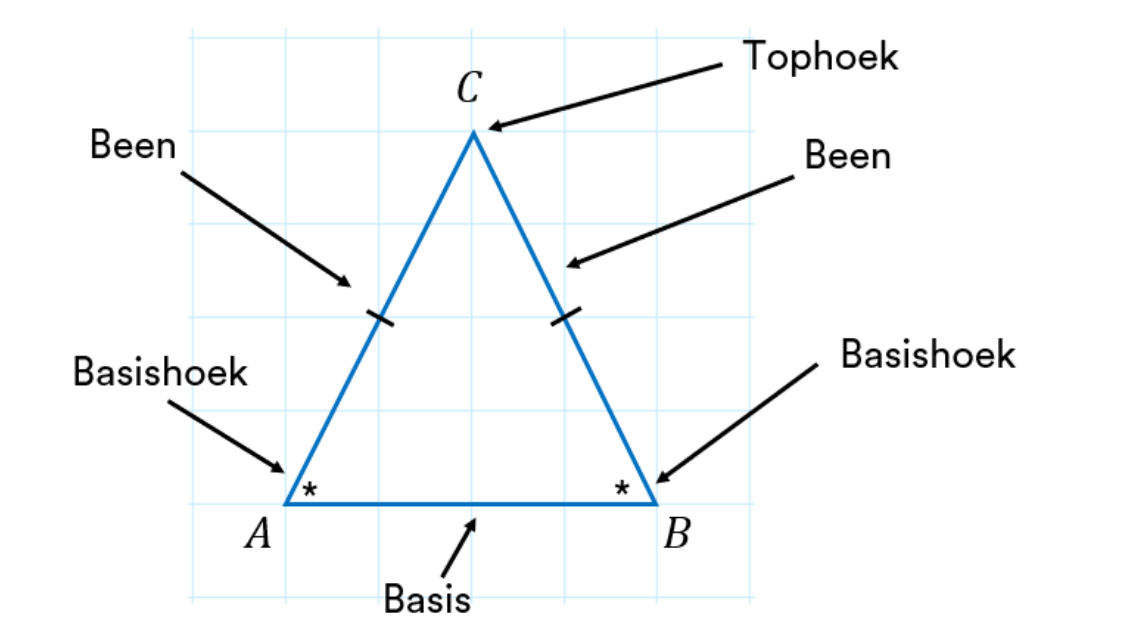
Voorbeelden van driehoeken zijn de gelijkzijdige driehoek (alle zijden gelijk), de gelijkbenige driehoek (twee zijden gelijk) en de ongelijkzijdige driehoek (geen zijden gelijk).
Voordelen van de driehoek in constructies zijn stabiliteit, efficiënt materiaalgebruik en eenvoudige berekeningen.
Voor- en Nadelen van Driehoeken in Constructies
Hieronder een tabel met de voor- en nadelen:
| Voordelen | Nadelen |
|---|---|
| Stabiel | Kan complexer zijn in ontwerp dan rechthoeken |
| Efficiënt materiaalgebruik | Minder interne ruimte |
Veelgestelde vragen:
1. Wat is de som van de hoeken in een driehoek? 180 graden.
2. Wat is een rechthoekige driehoek? Een driehoek met een hoek van 90 graden.
3. Wat is de stelling van Pythagoras? a² + b² = c² (voor rechthoekige driehoeken).
4. Hoe bereken je de oppervlakte van een driehoek? (basis * hoogte) / 2.
5. Wat is een gelijkzijdige driehoek? Een driehoek met drie gelijke zijden.
6. Wat is een gelijkbenige driehoek? Een driehoek met twee gelijke zijden.
7. Wat is een ongelijkzijdige driehoek? Een driehoek met geen gelijke zijden.
8. Hoe construeer je een driehoek met passer en liniaal? (beschrijving van de constructiestappen).
Tips en trucs: Gebruik een geodriehoek voor het tekenen van nauwkeurige driehoeken.
De driehoek, een ogenschijnlijk eenvoudige vorm, is een fundamenteel element in geometrie, constructie, design en vele andere disciplines. Het begrip van de eigenschappen en toepassingen van driehoeken is essentieel voor iedereen die geïnteresseerd is in wiskunde, wetenschap en techniek. Van de stabiliteit die het biedt in bouwconstructies tot de elegantie die het toevoegt aan kunstwerken, de driehoek blijft ons fascineren met zijn veelzijdigheid en kracht. Door de voortdurende studie en exploratie van deze vorm kunnen we nieuwe en innovatieve toepassingen ontdekken en de grenzen van onze kennis blijven verleggen. Duik dieper in de wereld van de driehoek en ontdek de eindeloze mogelijkheden die deze fascinerende vorm te bieden heeft.
Het charmante dorpsleven ontdekken
Mail merge in word de ultieme gids
Overwin elke uitdaging met de only easy day was yesterday poster













