Grenzkostenformel knacken Gewinnmaximierung im Business

Wie viel kostet es dich, *eine* weitere Einheit zu produzieren? Diese Frage ist der Schlüssel zur Gewinnmaximierung und die Antwort liegt in der Grenzkostenformel. Sie ist ein mächtiges Werkzeug für Unternehmen jeder Größe und Branche.
Die Berechnung der Grenzkosten, also der Kosten für die Herstellung einer zusätzlichen Einheit, ist essenziell für strategische Entscheidungen. Sie hilft dir, den optimalen Produktionspunkt zu finden, an dem deine Gewinne maximal sind. Verständnis der Grenzkostenberechnung ist somit essentiell für wirtschaftlichen Erfolg.
Die Grenzkostenfunktion liefert die Grundlage für fundierte Preisentscheidungen und Produktionsoptimierung. Sie erlaubt es Unternehmen, ihre Ressourcen effizient einzusetzen und ihre Profitabilität zu steigern. Von der Produktionsplanung bis zur Preisgestaltung – die Grenzkostenformel ist ein unverzichtbares Instrument.
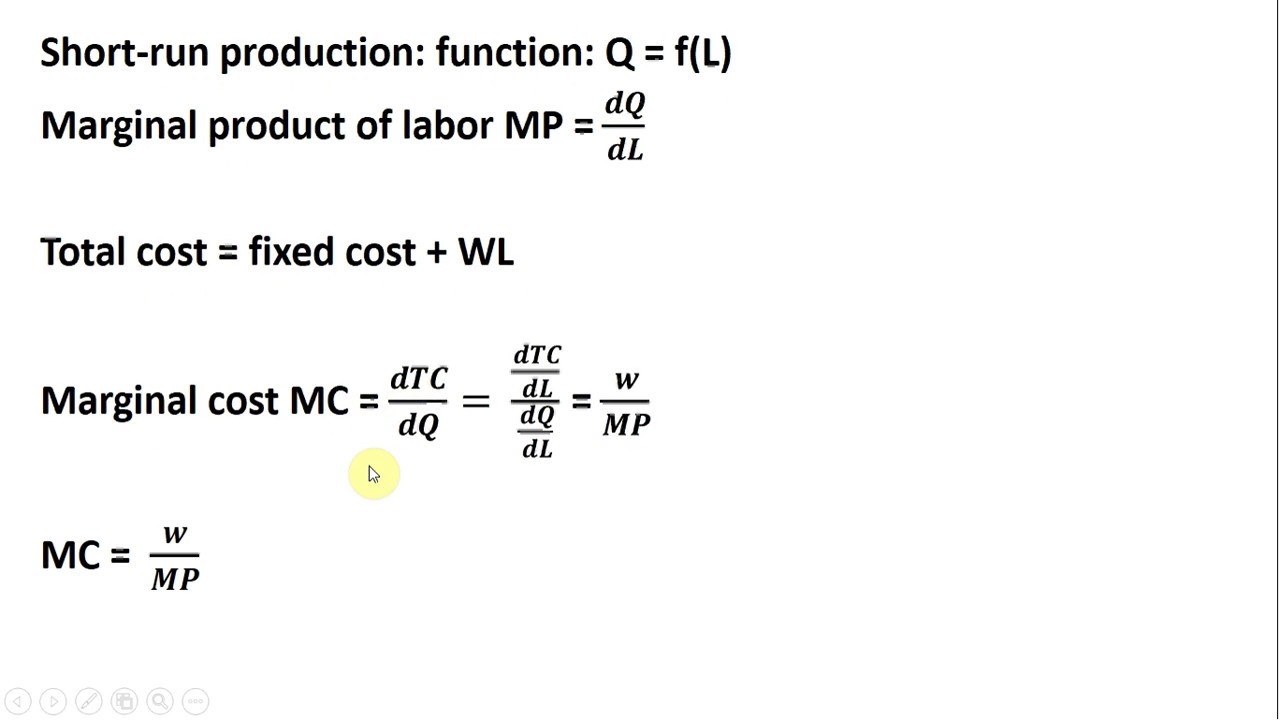
Die Formel für die Grenzkosten kann auf verschiedene Arten ausgedrückt werden, abhängig von den verfügbaren Daten. Sie lässt sich sowohl aus der Kostenfunktion ableiten als auch durch die Differenz der Gesamtkosten bei unterschiedlichen Produktionsmengen approximieren. Die Interpretation der Grenzkosten ist dabei stets die gleiche: die zusätzlichen Kosten für eine zusätzliche Einheit.
In diesem Artikel tauchen wir tief in die Welt der Grenzkostenformel ein. Wir betrachten ihre Definition, ihre Bedeutung, ihre Berechnung und ihre Anwendung in der Praxis. Von einfachen Beispielen bis hin zu komplexeren Szenarien – hier findest du alles, was du über die Grenzkostenformel wissen musst.
Die Grenzkostenrechnung hat ihre Wurzeln in der neoklassischen Ökonomie des späten 19. Jahrhunderts. Sie entstand aus dem Bedürfnis, die optimale Produktionsmenge zu bestimmen und den Einfluss von Skaleneffekten zu verstehen. Ein Problem der Grenzkostenberechnung ist die Schwierigkeit, sie in der Praxis präzise zu erfassen, da viele Faktoren die Kosten beeinflussen können.
Die Grenzkosten werden berechnet, indem die Änderung der Gesamtkosten durch die Änderung der Produktionsmenge dividiert wird. Beispiel: Wenn die Produktion von 100 auf 101 Einheiten die Gesamtkosten von 500€ auf 505€ erhöht, betragen die Grenzkosten 5€.
Vorteile der Grenzkostenformel sind: 1. Optimale Produktionsmenge: Sie hilft, die Produktionsmenge zu finden, bei der der Gewinn maximal ist. 2. Effiziente Ressourcenallokation: Sie unterstützt die optimale Verteilung der Ressourcen. 3. Fundierte Preisentscheidungen: Sie liefert wichtige Informationen für die Preisgestaltung.
Aktionsplan: 1. Kostenfunktion bestimmen. 2. Grenzkostenfunktion ableiten. 3. Optimale Produktionsmenge bestimmen. Beispiel: Ein Bäcker stellt fest, dass die Grenzkosten für ein zusätzliches Brot 0,50€ betragen. Solange er mehr als 0,50€ pro Brot erhält, steigert jedes zusätzliche Brot seinen Gewinn.
Vor- und Nachteile der Grenzkostenanalyse
| Vorteile | Nachteile |
|---|---|
| Optimale Produktionsmenge | Vereinfachtes Modell |
| Effiziente Ressourcenallokation | Schwierige Datenerhebung |
| Fundierte Preisentscheidungen | Ignoriert qualitative Faktoren |
Bewährte Praktiken: 1. Regelmäßige Überprüfung der Kosten. 2. Berücksichtigung aller relevanten Kosten. 3. Verwendung von Software zur Berechnung. 4. Sensitivitätsanalyse durchführen. 5. Berücksichtigung externer Faktoren.
Herausforderungen und Lösungen: 1. Ungenaue Daten: Lösung: Datenqualität verbessern. 2. Komplexe Kostenstrukturen: Lösung: Vereinfachte Modelle verwenden. 3. Veränderliche Marktbedingungen: Lösung: Regelmäßige Anpassungen.
FAQs: 1. Was sind Grenzkosten? 2. Wie berechnet man sie? 3. Was ist die optimale Produktionsmenge? 4. Wie hilft die Grenzkostenformel bei der Preisgestaltung? 5. Was sind die Grenzen der Grenzkostenanalyse? 6. Wie berücksichtigt man externe Faktoren? 7. Welche Software kann man verwenden? 8. Wie oft sollte man die Grenzkosten berechnen?
Tipps: Nutzen Sie Software zur Automatisierung der Berechnungen. Berücksichtigen Sie sowohl variable als auch fixe Kosten. Führen Sie regelmäßige Überprüfungen durch.
Die Grenzkostenformel ist ein mächtiges Werkzeug für Unternehmen jeder Größe. Sie bietet einen klaren Weg zur Gewinnmaximierung und effizienten Ressourcenallokation. Durch das Verständnis der Grenzkosten und ihre Anwendung können Unternehmen fundierte Entscheidungen treffen und ihren Erfolg langfristig sichern. Nutzen Sie die Grenzkostenformel, um Ihr Unternehmen auf das nächste Level zu bringen und Ihre Profitabilität zu maximieren. Es ist ein kontinuierlicher Prozess, der Anpassung und Überarbeitung erfordert, aber die Vorteile einer optimierten Produktion und Preisgestaltung sind die Mühe wert. Beginnen Sie noch heute mit der Analyse Ihrer Grenzkosten und entdecken Sie das volle Potenzial Ihres Unternehmens.
Sturm der liebe vorschau aktuelle spoiler und handlungsgeruchte
Ride sharing in costa rica uber und lyft alternativen
Taylor swift wien tickets jagen der ultimative guide


:max_bytes(150000):strip_icc()/marginal-cost-of-production-4193224-FINAL-1c530f2a6d1846cdaf442aff7b8d66eb.png)









